Radio Levania, émettre dans l’espace de la désidération

Chers passagers, nous vous invitons maintenant à rejoindre le complexe du rez-de-chaussée, où à vous installer à l’étage – la mutation va bientôt commencer. Pour le bon déroulé de cette séquence nous vous engageons à trouver un endroit confortable et à svous asseoir pour écouter dans les meilleures conditions.

Vous qui entrez, n’abandonnez pas tout espoir, ni toute mélancolie
Entrez dans l’espace de la désidération
Entrez dans ce lieu où diagnostiquer le vertige de la perte des étoiles
Quand l’émerveillement pour le cosmos se retourne en mélancolie
Nous faisant sentir tout ce qui est perdu
Quand le plaisir renouvelé des choses spatiales dit aussi la tristesse, et l’abandon
Et la volonté de retrouver quelque chose d’indistinctement cosmique
Et de goûter la douceur et l’amertume du miel laiteux des étoiles
Voilà la désidération qui s’étoile bientôt en affect, en syndrome, en pensée, en fiction, en recherches spatiales, endocosmologiques, tous azimuts
Entrez dans ce lieu fait aussi pour appréhender une voie qui mène à un état autre
Un lieu pour réinventer l’espoir et la mélancolie,
Un lieu pour transitionner, avec les étoiles, les humains, les mondes,
Un lieu pour appréhender l’affect de la désidération, et muter avec lui
Un lieu pour initier cette découverte et cette transmutation
Un lieu pour appréhender l’avenir
Un lieu pour découvrir
Une onde
Un chemin
Des voix dans le cosmos
Un lieu pour voir, un lieu pour écouter, un lieu pour dormir, un lieu pour rêver
Avec l’aide de la cellule Cosmiel
Avec la voix de Radio Levania
Vous qui entrez, n’abandonnez pas tout espoir, ni toute mélancolie.

Chaos is a seemingly random, chance and irregular motion that occurs only in non-linear and non-accumulable dynamical systems, which are sensitive to initial conditions. Since the tiny errors in chaotic motion grow rapidly with time, the motion at this point can be quite different from what it would be without these errors. This means that long-term prediction of chaotic motion in general is very difficult. It also means that chaotic motion has many new properties that the usual dynamical systems do not have. This has led to widespread interest in the study of chaos in various areas of physics. In general relativity, the geodesic motion of particles in a generic Kerr-Newman black hole spacetime is integrable and there is no chaos in this system. In order to study chaotic motion in general relativity and to ensure that the dynamical system describing the motion of the mass is integrable, it is necessary to resort to some spacetime with a complex geometry or to introduce additional interactions. Along this spirit, the chaotic motions of particles have been studied in the multi-black hole spacetimes, the perturbed Schwarzschild spacetime, and in the non-standard Kerr black hole spacetime described by MankoNovikov metric.

The study of chaotic behavior of the geodesic motion of particles has now involved several spacetime contexts, and the main interest of researchers in these systems is to use and further develop coordinate invariant descriptions and metrics of chaotic behavior to make them applicable to general relativity where space and time are not absolute. It has been recently shown that using the Melnikov method to identify chaotic behavior in geodesic motion perturbed by the minimum length effect around a Schwarzschild black hole, there is Smale horseshoes chaotic structure in the phase space. Based on the Melnikov method, the existence of a critical amplitude affecting temporal chaos is demonstrated by studying the thermodynamic chaos of RN-AdS black holes immersed in Perfect Fluid Dark Matter, while spatial chaos is always present regardless of the perturbation intensity. It has also been tentatively proved that the chaotic behavior of particles near the black hole has quantum gravitational effects. In addition, chaotic phenomenon was also investigated for the pinning particles in Kerr spacetime. More interestingly, chaos in loop string dynamics has been found in the asymptotically flat Schwarzschild black hole spacetime, in the AdS-Schwarzschild black hole and in the AdS-Gauss-Bonnet black hole spacetime after the introduction of loop strings instead of point particles.

In recent studies, a number of violations of the chaos bound have been discovered. The static equilibrium of charged probe particles around a black hole can be provided by the Lorentz force. In Ref., Zhao et al. considered the contribution of the sub-leading terms in the expansion of the near-horizon regions and investigated the chaotic bound in the nearhorizon regions using the effective potential. It is found that the Reissner-Nordstrom and Reissner-Nordstrom-AdS black holes satisfy this bound, which is violated in a large number of charged black holes. In their study, they only considered the radial contribution. In fact, since angular momentum affects the effective potential and increases the magnitude of the chaotic behaviour of the particles, angular momentum also has an effect on the Lyapunov exponent. In consideration of the above, Lei et al. again studied the chaos bound in the near-visible region of Reissner-Nordstrom and Reissner-Nordstrom-AdS black holes. It is found that the bound is violated in the near-visible region when the angular momentum of the charge and particles of the black hole is large. In rotating charged black holes, the existence of a violation of the bound was also found by calculations of the effective potential.

Taking into account the motion of charged particles on the equatorial plane of the torus-like black hole, the calculation of the eigenvalues of the Jacobi matrix, leads to a general expression for the Lyapunov exponent. The metric of the black hole is:

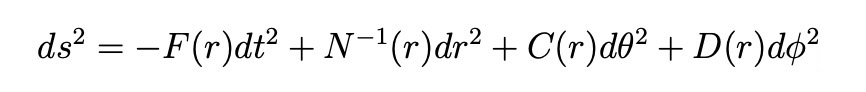
When a charged particle moves around a black hole, its Lagrangian can be expressed as:

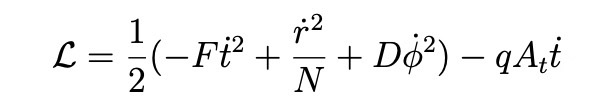
Further exploration of the variation of the black hole chaos bound is in the near-horizon region and at a certain distance from the horizon. For the observation, we perform numerical calculations for the Lyapunov exponent at the equilibrium orbits and the surface gravity at the black hole horizon. When the charge value is fixed, the variation of the angular momentum has a significant effect on the value of the Lyapunov exponent, which leads to the change of the bound. There is no violation when the angular momentum is relatively small, i.e., the position of the equilibrium orbit is close to the black hole horizon. As the angular momentum increases, the bound is violated at a certain distance from the black hole horizon. There exists a special value of angular momentum, when the angular momentum is larger than this value, the violation phenomenon appears. It is observed that this special value increases with the increase of the charge value.

The variations of the chaos bound of the torus-like black hole in the near- horizon region and in the region at a certain distance from the black hole horizon were studied. The effects of different charges and different angular momenta on the equilibrium position of the orbit were first investigated. It is found that when the charge value is fixed, the orbital equilibrium position gradually moves away from the black hole horizon with the increase of angular momentum. When only the charge parameter is considered, the orbital equilibrium position parameter decreases with the increase of charge value, which is the same as the effect of charge on the black hole horizon. Subsequently, the Liapunov exponent is calculated by the Jacobi matrix, and further study reveals that the angular momentum has a great influence on the value of Liapunov exponent. The chaos bound is not violated in the near-horizon region; and with the increase of angular momentum, the bound is violated at a certain distance from the black hole horizon.

In recent years, due to an intrinsic non-linearity of General Relativity, the dynamic of chaos has already been one of the great focus in relativistic systems. On account of the susceptivity to the initial condition, chaos is a kind of random motion and cannot be predicted in deterministically and nonlinearly dynamic systems, leading in turn to appeal to many researchers spread deep exploration to chaotic phenomena.

However, chaos always emerges so as to expand the research to some complicated space-time backgrounds, for example, exploring the motion of the charged particle around a black hole including quasi-topological electromagnetism, a scalar particle coupling to the Chern–Simons invariant in the Kerr black hole, and a particle among the Rindler space in a 4-Dimension black hole having spherically symmetric construction. These researches reveal that the main reason for the occurrence of chaos is that the equation of motion is variable-inseparable and the corresponding nolinear dynamical system is not integrable, which is led by those complicated couplings. In addition, although the dynamic of a particle is integrable, it has also been proved that the chaotic phenomena can occur in a certain potential, for example, a massless and chargeless particle with the addition of harmonic perturbation in a very near horizon region.

Until now, the motion of a string in space-time has also attracted the interest of many travelers, which is rapidly becoming a vigorous area of research in string theory. The more complex and more intriguing behaviors of the motion of the string can be exhibited via the inherent outstretched nature of string. Aspects of closed strings dynamics in the Schwarzschild black hole with the foundational background have been profoundly studied. As pointed out, the effect of the parameters of the charge Reissner-Nordstrom black hole or the anti-de Sitter(AdS) Gauss-Bonnet black hole causes that the dynamical behaviors of the closed string generate a special transformation. There is potential significance to discuss the conversion from order to chaos and the condition of transformation. Moreover, some also pay close attention to chaos bound and its violation.

At a classical level, the motion of one string in miscellaneous curved space-time backgrounds is non-integrable. The dynamics of the string behave features of chaotic motion, even on radially symmetric backgrounds. In contrast, the motion of a test particle is integrable in most radially symmetric backgrounds. Understanding the difference of motion between a string and a particle in the cosmological or gravitational backgrounds may give some enlightening views and reveal various problems which are associated with classical gravitational singularities. Another motivation to investigate string dynamics in black holes arises from growing interest in chaos near black holes, which is aroused by more complex quantum chaos through the analysis of the dynamics of relatively simple black holes. Chaos of one string around a black hole is an important topic of contemporary research in physics. As far as we are aware, the characteristic of the chaos in the vicinity of a black hole is linked to the character of the black hole. Hence, investigating as many various black holes as possible may be available to comprehend the chaos phenomena more clearly. However, in masses of curved time-space contexts, string theory is not capable of being resolved analytically. It is widely advised that such kinds of integrability can be stretched to the field theory via taking advantage of the AdS/CFT theory duality.

Valid chaos indicators are crucial for discussing the evolutionary process of chaotic systems. We call for the tools of chaos indication, such as spectrum analysis, Poincare sections, Lyapunov exponents, maximal Lyapunov exponents, fast Lyapunov indicators, fractal basin boundaries method, etc. There are advantages and disadvantages to just about every known chaos indicator. For an integrable system, the four-dimensional phase space can be reduced to a three-dimensional space using the energy constraint. Then a two-dimensional plane in the three-dimensional energy manifold intersecting the family of two-dimensional tori in the transverse direction would constitute a Poincaré section.

By using numerous numerical techniques, we have studied the chaotic dynamics of classical string motion in the quintessential Bardeen-AdS black hole. We have investigated the conditions for the generation of chaos and its properties over the extended phase space of the quintessential Bardeen-AdS black holes. By performing Poincaré Sections and computing the maximum Lyapunov exponent, an exploration of the chaotic dynamics of the string lying in the vicinity of a Bardeen-AdS black hole has been carried out. There is a cosmological horizon present when the normalization constant a is sufficiently large and which is separated by some distance from the event horizon so that there is no minimum limit on the mass of a Bardeen-AdS black hole. The chaotic dynamics behavior of the string is impervious to the magnetic monopole charge. From investigation, the normalization constant performs an instrumental part in the chaotic dynamics of classical string motion. We have remarked that the motion of the ring string in the context of a Bardeen-AdS black hole is weakly chaotic and becomes progressively more chaotic as we increase the normalization constant.

Depuis des temps immémoriaux, on incube des rêves
On vient dans des lieux chargés de magie et d’espoir
En s’allongeant auprès des pierres sacrées
On vient dormir dans ces lieux merveilleux
Pour rêver de ces rêves messagers
De ces rêves guérisseurs
De ces promesses sibyllines

Depuis des temps immémoriaux, on cherche dans ces rêves
La révélation d’un sens perdu
On cherche l’état de cosmiel où tout le cosmos
Inspire et respire avec nous
Inspire et respire avec nous

Depuis des temps immémoriaux
je parle à ceux qui ont perdu le sens des astres.
Fermez maintenant les yeux et laissez ma voix vous guider à nouveau jusqu’à eux
Depuis longtemps votre corps sait atteindre cet état entre la veille et le sommeil
où il est le plus prêt à recevoir des vérités interstitielles

Laissez vos yeux se détendre, votre souffle entrer et sortir, et écoutez ma voix,
la voix de Radio Levania
Les nébuleuses entrent en vous, sortent de vous
Les astres vont bientôt apparaître sous vos paupières
Les nébuleuses entrent et sortent de vous, lentement,
Vous formez peu à peu en vous un cosmos respirant
Les particules d’étoiles se fondent en un souffle
Elles passent en vous et hors de vous
Lentement

Jusqu’à ce que, dans ce ciel vous tourniez la tête vers un ciel encore plus infini
D’étoiles, de comètes formées des mêmes entités, transportant votre même essence
Des ondes, des particules dont vous êtes la résultante, vous traversent,
Vous, créatures – créatrices du futur, vous sentez le cosmos s’étendre en vous.
Il est temps maintenant de rêver…